数1 因数分解 628789-数1 因数分解 難問

 （分解质因数也称分解素因数）求一个数分解质因数，要从最小的质数除起，一直除到结果为质数为止。 分解 质因数 的方法是先用一个合数的最小 质因数 去除这个合数，得出的数若是一个质数，就写成这个合数相乘形式；若是一个合数就继续按原来的方法，直至最后是一个质数 。多項式を計算してから、素因数分解すると因数分解できるよね。 多項式を計算すると、 ＝18 だね。これを素因数分解の筆算をすると、 になるね。 2 だね。 答えは合っているけど、、、 多項式のかけ算とたし算を計算したのに、因数分解して、もう一度かけ算の式にしているから、なんか あとは後ろの4つの項からなる式を因数分解して共通因数でくくれば終わり。 共通因数が出てこなければ因数分解できないから，後ろ4つの項を因数分解すると a b − 1 が現れることは確定している。 これを考えれば比較的楽に因数分解できるだろう。 （ 与 式 ） （ 与 式 ） = ( a b − 1) c a 2 b − a b 2 − a b = ( a b − 1) c ( a b − 1) ( a − b) = ( a b − 1) { c ( a − b

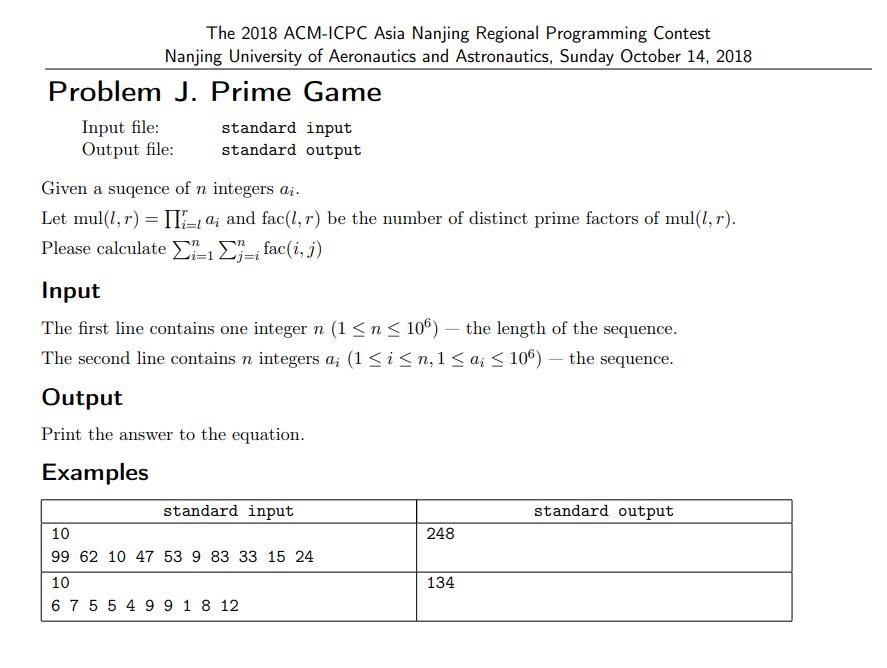
Prime Game 质因数分解 线性筛 思维 Xxiaoyu 博客园

数1 因数分解 難問

数1 因数分解 難問- よって解αの候補は α＝±1，±2，±4，±8 の8通りとなりますのでやりやすそうなのから順に代入していきましょう。 P (1)=1368=0 早速、解が一つ出てきました。 後は前述した通り、2次方程式と組み合わせにして因数分解すればOKです。 今回は早急に解が出てきてしまいましたが2つ目、3つ目の計算で解が出てくることもあります。 しかしいずれにせよ上の定理を後は因数分解の練習は必要無くなる、と良いですね。 ちょっと特殊な因数分解 ④の因数分解は、今までの方法ではできないものです。 その中でも因数定理を使う物は省いて、1つだけ、紹介しておきます。 例「\(\hspace{10pt} x^4x^21\hspace{4pt}\)を因数分解せよ。

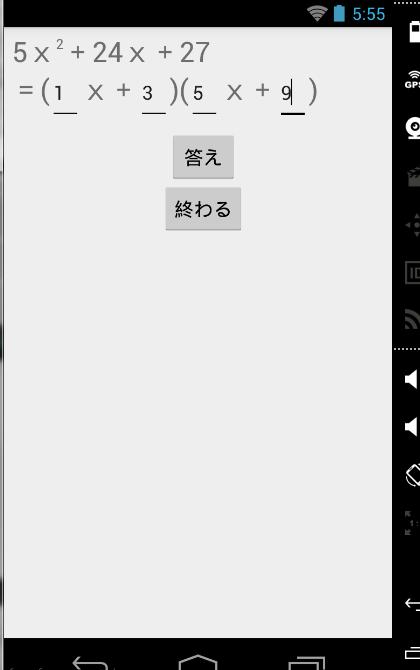
脳トレ数学 因数分解 展開 安卓下载 安卓版apk 免费下载

動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru 因数分解の応用 ここからは、基本①~③だけでは解けない問題について考えてみましょう。 例えば、\(3mx^29mx6m\)は、因数分解の基本①~③には当てはまっていませんよね。 こういう場合は、基本①→基本②→基本③の順に考えていけば良いです。 （1）用分解质因数的方法，把这两个数公有的质因数和各自独有的质因数相乘。 （2）用短除法的形式求。 （3）特殊情况：如果两个数是互质数，那么这两个数的积就是它们的最小公倍数。 如果两个数中较大的数是较小的数的倍数，那么较大的数就是这两个数的最小公倍数。 已赞过 已踩过 你

因数分解とは 『因数分解』 とは 数を複数の数の積で表すこと といい、積で表した一つ一つの数を "因数" といいます。 たとえば「12を因数分解せよ」と言われれば、「12＝2×2×3」や「12＝4×3」「12＝6×2」と答えます。 因数がすべて "素数" になる将一个正整数分解质因数。例如：输入90，打印出90=2*3*3*5。 程序分析：对n进行分解质因数，应先找到一个最小的质数k，然后按下述步骤完成： 如果这个质数恰等于n，则说明分解质因数的过程已经结束，打印出即可。 如果nk，但n能被k整除，则应打印出k的值，并数と式 高1数学単項式の乗除のやり方、指数法則を理解しよう！ 数と式 まとめ高校で学習する因数分解のやり方をぜんぶ解説！ 平方根 1 平方根分母の有理化のやり方はこれでバッチリ！ 数と式 327 対称式の変形まとめ！基本公式を覚えてサクサク計算

 こんにちは！櫻學舎講師の山口です。 皆さんは数学の問題を解いていて、「この高次式を因数分解できれば・・・」と思ったことはありませんか？ 今回は高校の数学でとても役に立つ組み立て除法について書きたいと思います。 1．組み立て除法とは 組み立て除法とは高次式を簡単に因数 1751 分解因数 （ 递归 ） 最新发布 木静音yy的博客 16 281 描述 给出一个正整数a，要求 分解 成若干个正整数的乘积，即a = a1 * a2 * a3 * * an，并且1 < a11次式の因数分解は，共通因数でくくる変形があるだけですから，共通因数を考えます． (ab) x (ab)(a−b) =(ab)(xa−b) （答）

質因數分解法與標準分解式 Youtube

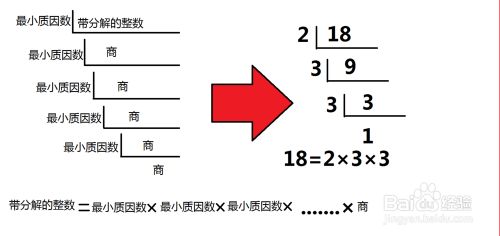
分解素因数的方法 百度经验

 蓝桥杯 试题 基础练习 分解质因数 思路：我们可以先求出从2到b之间所有的素数，把这些素数插入数组，然后每次从头遍历这个素数数组,如果当前的数能整除素数，那么跟新新的当前的值，及除以素数，然后从头PollardRho 大质因数分解，一般可以结合 MillerRabin 素数判定，一般适用于 的情况。 由于其实现上差异较大，不同的做法在时间上差距极大。 以 洛谷 P4718 模板PollardRho算法 该题为例，需要针对每个数找出最大的质因数，出题人本意考察的是在原始的 PollardRho 递归搜索程序上进行剪枝来优化时间，实际上通过 github用户"nyaannyaan"模板库中的代码 ，即使不做剪枝，直接做就是一个数的约数，并且是质数，比如8=2×2×2，2就是8的质因数。 12=2×2×3，2和3就是12的质因数。把一个式子以12=2×2×3的形式表示，叫做分解质因数。 16=2×2×2×2,2就是16的质因数， 把一个 合数 写成几个质数相乘的形式表示，这也是 分解 质因数 。 1

四次式因數分解 Slobo

如何找出一个数的因数 11 步骤

因数分解を行う式を電卓に入力し「因数分解」ボタンを押してください。 置き換えや公式を連続して使うなどの複雑な因数分解では途中式も表示されますので解き方の手順がわかります。 この電卓は中学で習う因数分解に対応しています。 3次式などの x^41を複素数の範囲で因数分解しなさいがよく分かりません。教えてください。 （）（）（）（）になるので x^41=0を解こうとしましたがx^2＝＋－i となって解けません。なぜですか？ また式変形で ( )^2( )^2 にするらしいんですがこの発想はどこからくるんですか？ よく分からないので詳しく具体例で学ぶ数学 > 計算 > 因数分解公式一覧（全22個） 最終更新日 ～中学数学で最初に習う、基本的な公式～ x 2 ( a b) x a b = ( x a) ( x b) x 2 2 x y y 2 = ( x y) 2 x 2 − 2 x y y 2 = ( x − y) 2 x 2 − y 2 = ( x y) ( x − y) ～たすきがけの公式～ a c x 2 ( a d b c) x b d = ( a x b) ( c x d)

数论专题 因数就是这个样儿 每日头条

数学 質問解答 ３文字 の因数分解 パート１ 高校数学 数a 因数分解 質問ありがとうございました 行間 ぎょうのあいだ 先生

適当な公式を用いて，次の式を因数分解せよ。 \ 10 次の式を因数分解せよ。 de d e de de d e \ de\ 11 次の式を因数分解せよ。 数学Ⅰ 数と式（因数分解） 演習プリント 因数分解の公式1：x 2y 2 =(xy)(xy) 中学生の皆さんが真っ先に身に着けている公式が x 2 y 2 =(xy)(xy) です。 後に紹介する2種類の公式ほど長いわけでは無いため、この式だけは身につけているというパターンが多いのが特徴です。LINE Pocket 高校で学習する因数分解は複雑で難しい！ ！ 「わからないので教えてください」と質問をいただくことの多い単元でもあります。 なので、今回の記事では高校1年生で学習する因数分解のやり方についてパターン別にまとめておきます。 解き方の分からない因数分解に出会ったときには、この記事を解き方の辞書代わりに使ってもらえると嬉しいです (^^)

Scratch3 0编程与数学 求最大公因数 2短除法 Scratch 状课网

腾讯视频

事实上的结论是：（1 1）×（2 1）= 6个。 即某一自然数的约数个数是它各质因数的次数分别加1相乘的积！ 那么，根据上述结论， 我们将180进行分解，具体如下：分解质因数只针对合数。（分解质因数也称分解素因数）求一个数分解质因数，要从最小的质数除起，一直除到结果为质数为止。分解质因数的算式叫短除法，和除法的性质相似，还可以用来求多个数的公因式。 扩展资料 因为1没有质因子，1与任何正整数（包括1本身）都是互质。 正整数的因数動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru

Studydoctor平方の差を利用する因数分解 数 Studydoctor

互质是什么意思 又叫互素 真问网

因数分解したい式を入力してください。 因数分解電卓 複雑な式を単純な因子の積に変換します。 この因数分解電卓は、任意の変数を含む多項式だけでなく、より複雑な関数を因数分解することができます。 数式の書式を表示 python入门级别算法系列 1 分解质因数 1题目：分解质因数 将一个正整数分解质因数，即分解为由若干个质数相乘的结果，例如输入90,打印出 ， 其中2、3、5都是质数。 该题目思路比较简单，只需要用while for循环即可解决，适合新手入门python进行练习，本文将由易到难介绍几种实现思 最后要告诉大家的是找两个数公有的质因数就是要找这两个数的最小公倍数，如下图所示。 图 总结： 1 /1 1分解质因数有两种方法，一种想乘法，还有一种短除法。 2相乘法写成几个质数相乘的形式，实际运算时可采用逐步分解的方式。 3短除法是从最小的质数除起，一直除到结果为质数为止

高校数学 因数分解公式と3次式の因数分解 A B C 3abc 受験の月

10 5 因式分解 Ppt Download

整数分解工具 整数分解工具 计算一个给定的自然数的质因数,也可以使用带 * / ^ !每个合数都可以写成几个质数相乘的形式。其中每个质数都是这个合数的因数，叫做这个合数的分解质因数。 分解质因数只针对合数。 把一个合数分解成若干个质因数的乘积的形式，即求质因数的过程叫做分解质因数。 分解质因数只针对合数。（分解质因数也称分解素因数）求一个数分解质因数，要从最小的质数除起，一直除到结果为质数为止。分解质因数的算式叫短的表达式。 分解结果将以递增的质因数乘积形式展示。 如果您的表达式为质数，结果将为该数本身。 如果需要检测一个数是否为质数，您应当使用 Prime Number Calculator （质数发生器和校验器），其支持更大的的数。 支持的函数和运算

51nod 1434 区间lcm 质因数分解 7391 Kid 博客园

3种方法来分解因式

因数分解しなさい ①25x 21 ②9x 26x1 ③x 2 12x27 ④axayxy ⑤x 2x90 ⑥x 222x121 ⑦x 2 8x ⑧2ax2a3x3 ⑨49x 236y 2 ⑩x 2 6xy9y 2 ⑪36x 227x ⑫4x 2 ax25a 2 因数分解 那么如何分解质因数呢？下面介绍用短除法分解质因数。 工具/原料 more 整数 质数表 方法/步骤 1 /4 分步阅读 短除法是先用一个除数除以能被它除尽的一个质数,以此类推,除到商是质数为止。 图 2 /4 写出短除号，待分解的整数是被除数，用能整除这个数的最小质数做除数。 图 3 /4 商如果是 经典算法详解（12）分解质因数 题目：众所周知，任何一个合数（因数不止是1和本身）都可以写成几个质数相乘的形式，这几个质数叫做这个合数的质因数。 例如，24=2×2×2×3把一个合数写成几个质数相乘的形式叫做分解质因数。 对于一个质数，他的质因数

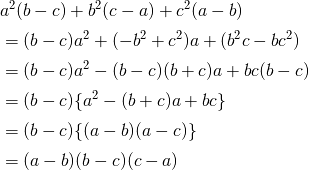
公式いろいろ 因数分解のいろいろな問題とその解き方 スタディクラブ情報局

质因数分解 3位数 儿童数学练习国小国中数学练习题题库下载列印 教学学习解答

 式中に分数が入る場合、因数分解をするために、まずは分数をなくす計算をしなくてなりません。 そのためには、まず分母に注目することから始めましょう。 分数をなくすことができれば、あとはいつもどおりの因数分解ができます。 1 分数が登場する因式分解工具可以将一个表达式分解成几个因式的积 首页 菜单 参与 平面图形计算器 立体图形计算器 质数生成器和校验器 分解质因数工具 斐波那契数 计算工具 伯努利数生成器 欧拉数计算器 复数计算器 阶乘计算器 伽马函数计算器 组合数计算器 分数计算器 统计工具 LaTeX 公式编辑器 数字

质因数分解 程序员大本营

数学 大数质因数分解定理 M0 的博客 Csdn博客

如何将一个大的数分解质因数 图片信息欣赏 图客 Tukexw Com

最小公倍数怎么求 4 5 6的最小公倍数怎么算 新课物网

用15的因数组成比例 西瓜视频搜索

四年级数学上册第5单元 倍数和因数 倍数和因数 教材内容说明冀教版素材下载 Word模板 爱问共享资料

1

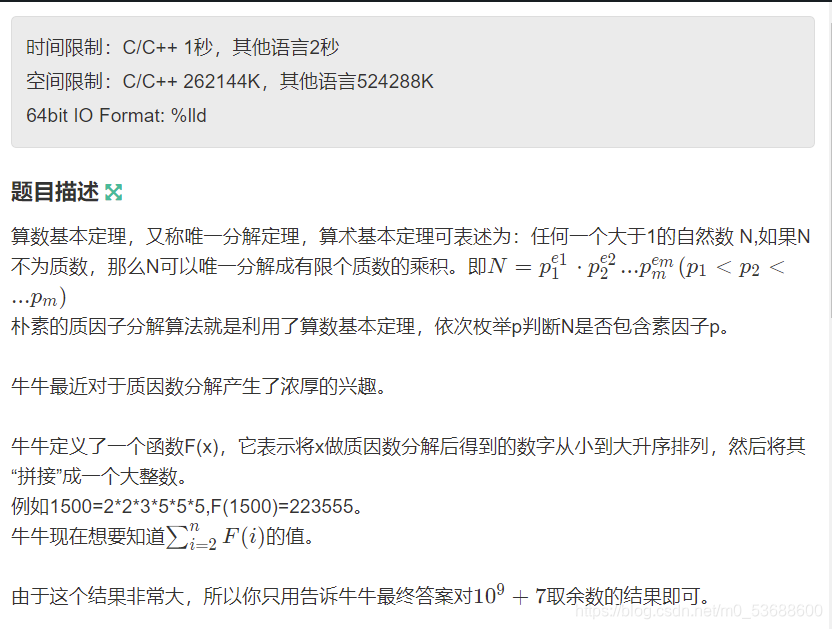
牛牛的质因数 M0 的博客 Csdn博客

怎么对一个数字进行因式分解 最有妙招网

看完这篇 终于可以和别人聊量子计算机了

Hdu 4135 Co Prime 容斥原理 质因数分解 C Dreamy的博客 程序员宅基地 程序员宅基地

高校数学 数1の因数分解について質問です 画像の問題の Yahoo 知恵袋

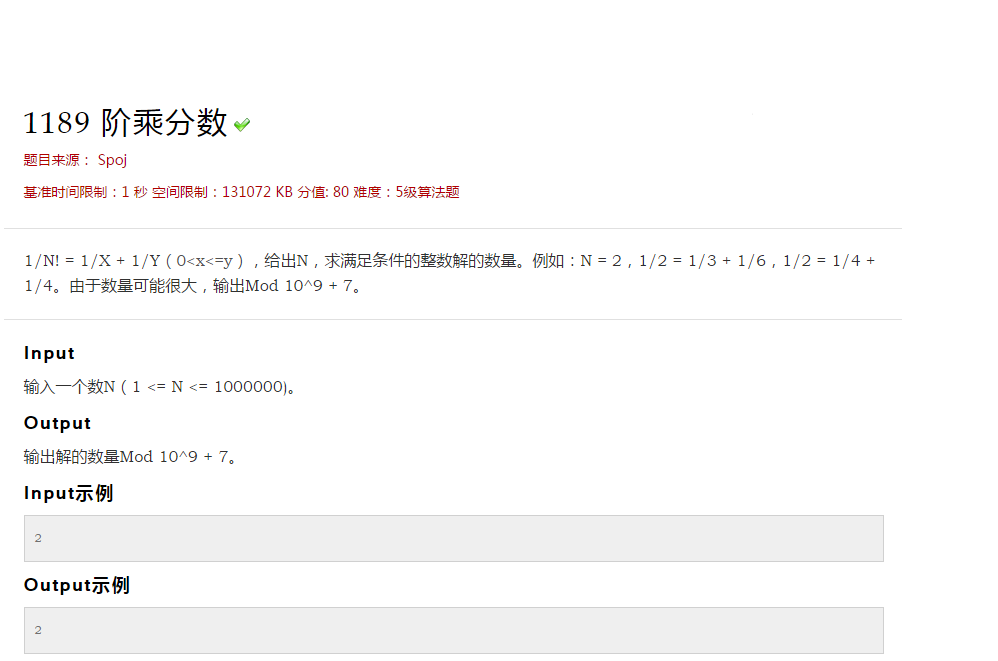
51nod 11 阶乘分数 阶乘质因数分解 Child Single 博客园

因数分解 腾讯视频

画像をダウンロード数1 因数分解 犬イラスト

3

质因数能分解出的最高个数 代号4101的专栏 Csdn博客 质数最多可以分解多少个

质因数分解 Kkxxzx的博客 程序员资料 程序员资料

Hpu暑期第五次积分赛f 辞树的质因数分解 Kk 18的博客 从前现在过去了再不来 程序员信息网 程序员信息网

用因数分解快速进行因式分解 三 哔哩哔哩

高中数学必修三 第一章算法设计几种典型设计题及解析 每日头条

驚くばかり因数分解中2 壁紙おしゃれトイレ

高校数学 数 １ ３次式の展開と因数分解 Youtube

质因数分解 3位数 儿童数学练习国小国中数学练习题题库下载列印 教学学习解答

初中数学基础 因式分解中的符号问题 没学好的学生抓紧来学

例題 利用質因數分解找出一個數所有的因數練習 數學 均一教育平台

Prime Game 质因数分解 线性筛 思维 Xxiaoyu 博客园

1到100质数表 100以内的质数图片 质数表口诀 最全知识分享

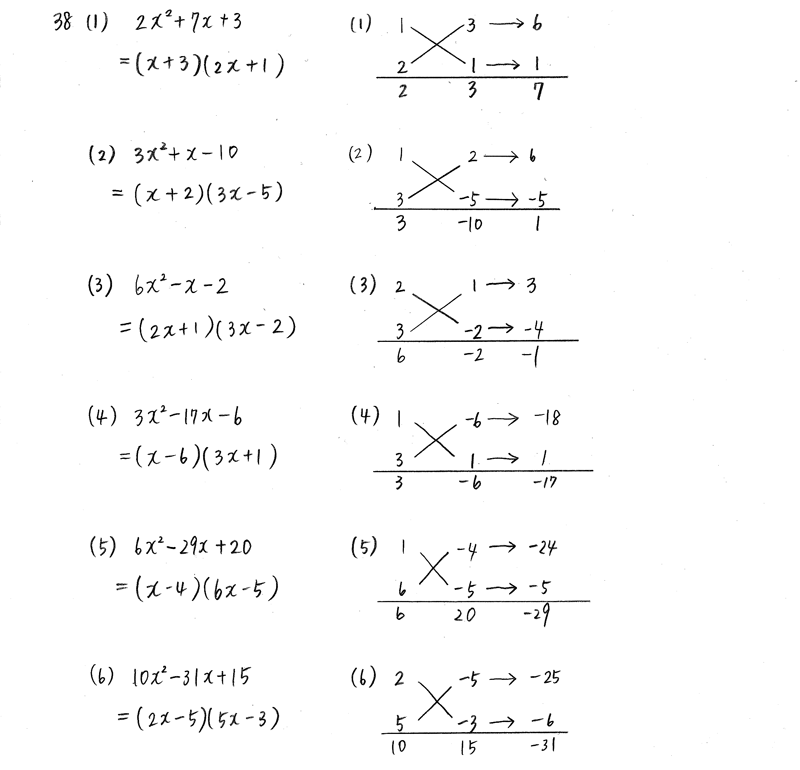
クリアー数学 数1 P13 ４ 因数分解 1

Catatan Tentang 夏まとめ 数学1 因数分解 Senior Clearnote

35分解质因数35如何分解质因数 天奇生活

数学 数と式 因数分解の手順 解答5 6 Youtube

数と不等式 １ 展開と因数分解１ 数i A 東大数学9割のkatsuyaが販売する高校数学の問題集

1x年春八年级数学下册第4章因式分解2 提公因式法教案北师大版下载 Word模板 爱问共享资料

在线分解质因数软件 因式分解计算器在线使用方法 爱惜日

约数个数问题的常规解法 18年11月19日 知乎

分解质因数是什么 初三网

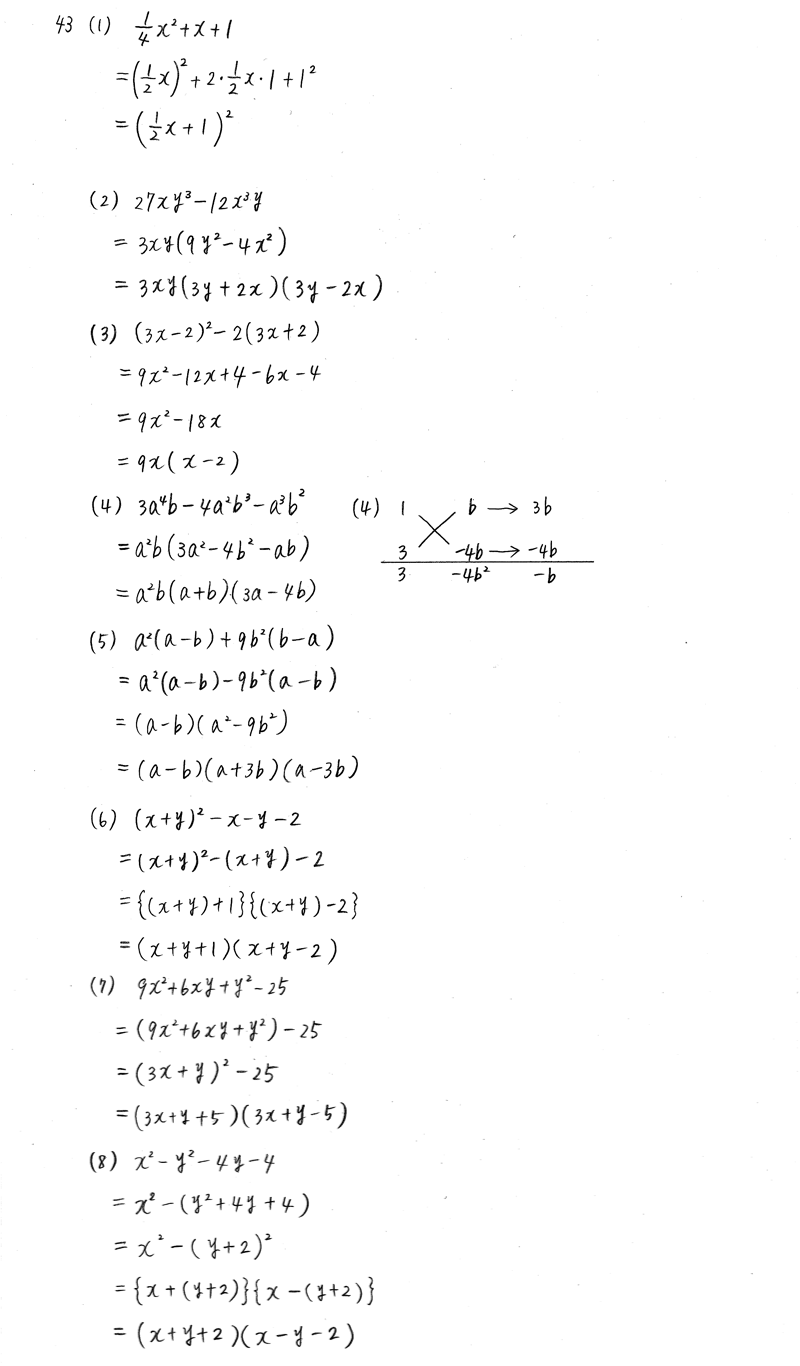
クリアー数学 数1 P14 ５ 因数分解 2

用因数分解快速进行因式分解 三 哔哩哔哩

Eju数学a 整数的性质 知乎

用因数分解快速进行因式分解 二 哔哩哔哩

３次の展開と因数分解 高校数学 数と式 Ex1 Youtube

质因数分解 3位数 儿童数学练习国小国中数学练习题题库下载列印 教学学习解答

脳トレ数学 因数分解 展開 安卓下载 安卓版apk 免费下载

觀念 什麼是質因數分解 數學 均一教育平台

高校入試 因数分解の難問を解説 難関高校の入試問題に挑戦しよう 数スタ

19 1 18 初一数学质因数分解大法1 质数2 从小到大 Site Engineer 工作日志 Facebook

质因数分解随机数生成器ios下载 质因数分解随机数生成器手机版 质因数分解随机数生成器1 2 1 华军软件园

什么是分解质因数 分解质因数的方法例子 豪友网

高校数学 複数の文字を含む因数分解は最も次数が低い文字で整理せよ 受験の月

质因数分解及代码 Youxin 博客园

高校数学 数 8 因数分解 基本編 Youtube

算法讲解 Scartch数学算法1之 分解质因数算法 少儿编程教程网

数検1級対策 1次 因数分解 因数分解 数検1級1次問題 T Co Jhkmz9uo4h Twitter

C 分解一个大数的素因数 Chenmeiqi的博客 Csdn博客

四年级数学上册第5单元 倍数和因数 分解质因数 教学建议冀教版素材下载 Word模板 爱问共享资料

题目出错 多种答案 唯一答案 质数 分解质因数重要性质和应用 每日头条

初中数学 因式分解的七大解题方式 一招搞定 教育频道 手机搜狐

100以内质因数分解代码 Littleasavakit的博客 Csdn博客

名探柯南在侦查一个特大盗窃集团过程中 获得藏有宝物的密码箱 密码究竟是什么呢 请看信息 Abcdef 每个字母表示一个数字

怎么对一个数字进行因式分解 最有妙招网

高校数学 数 10 因数分解 応用編 Youtube

64位以内rabin Miller 强伪素数测试和pollard Rho 因数分解算法的实现 Doc 文档分享网

数検１級の因数分解できる ３本勝負 Youtube

2 29 541 7919 素数 整数 合数 质数 因数 网易订阅

质因数分解 3位数 儿童数学练习国小国中数学练习题题库下载列印 教学学习解答

河野玄斗 冲击的答案 数检1级的公式答案也是错误的传说的因数分解太可怕了 哔哩哔哩 Bilibili

腾讯视频

Rsa 理论的正向思考过程 二 Yui 的严肃文

121分解质因数分解质因数 1 52 2 68 3 121 数学 魔方格

高校1年 数学i 因数分解 予習用練習問題 赤城 ᐡᐤᐡ

头条问答 18的因数有几个 14个回答

高校数学 因数分解の工夫 置き換え 受験の月

1

因式分解计算机

如何因式分解三次多项式 12 步骤

巧用质因数分解解决乘积问题 百度经验

免费计算器 附质因数分解功能 安卓下载 安卓版apk 免费下载

因数分解の公式まとめ一覧とその活用例 アタリマエ

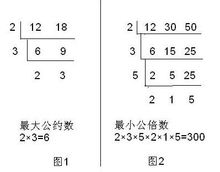
质因数分解及代码 Youxin 博客园

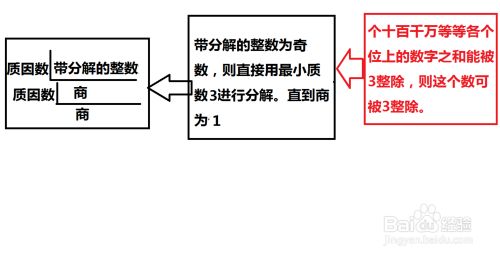
分解素因数的方法 百度经验

この赤枠のようになる理屈がわかりません 詳しく教えて頂きたいです Clearnote

P1075 质因数分解 编程猎人

怎么对一个数字进行因式分解 最有妙招网

质因数分解 Sac E 1 一道中档题factorial 代码天地

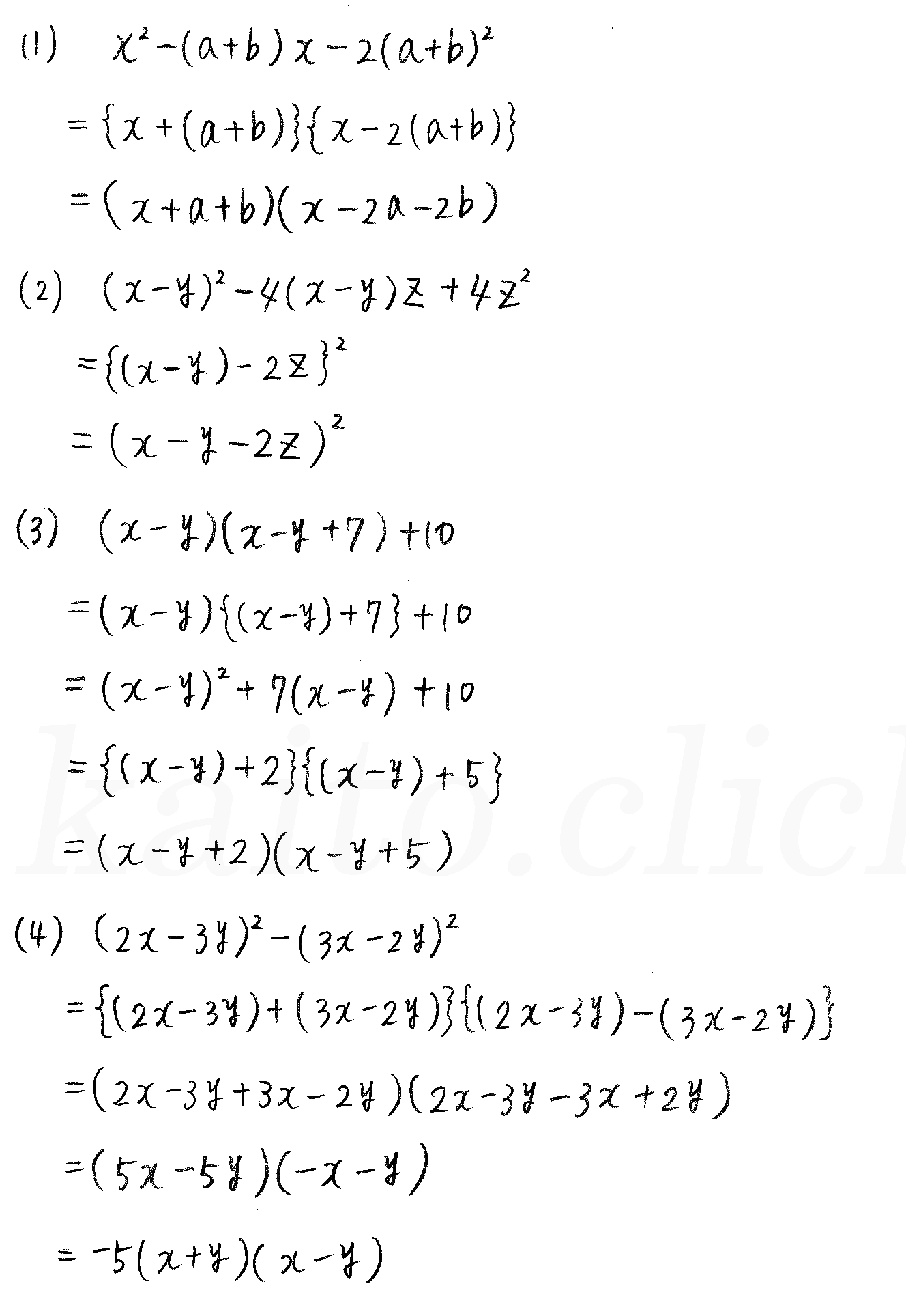
改訂版 クリアー数学 P15 ５ 因数分解 2

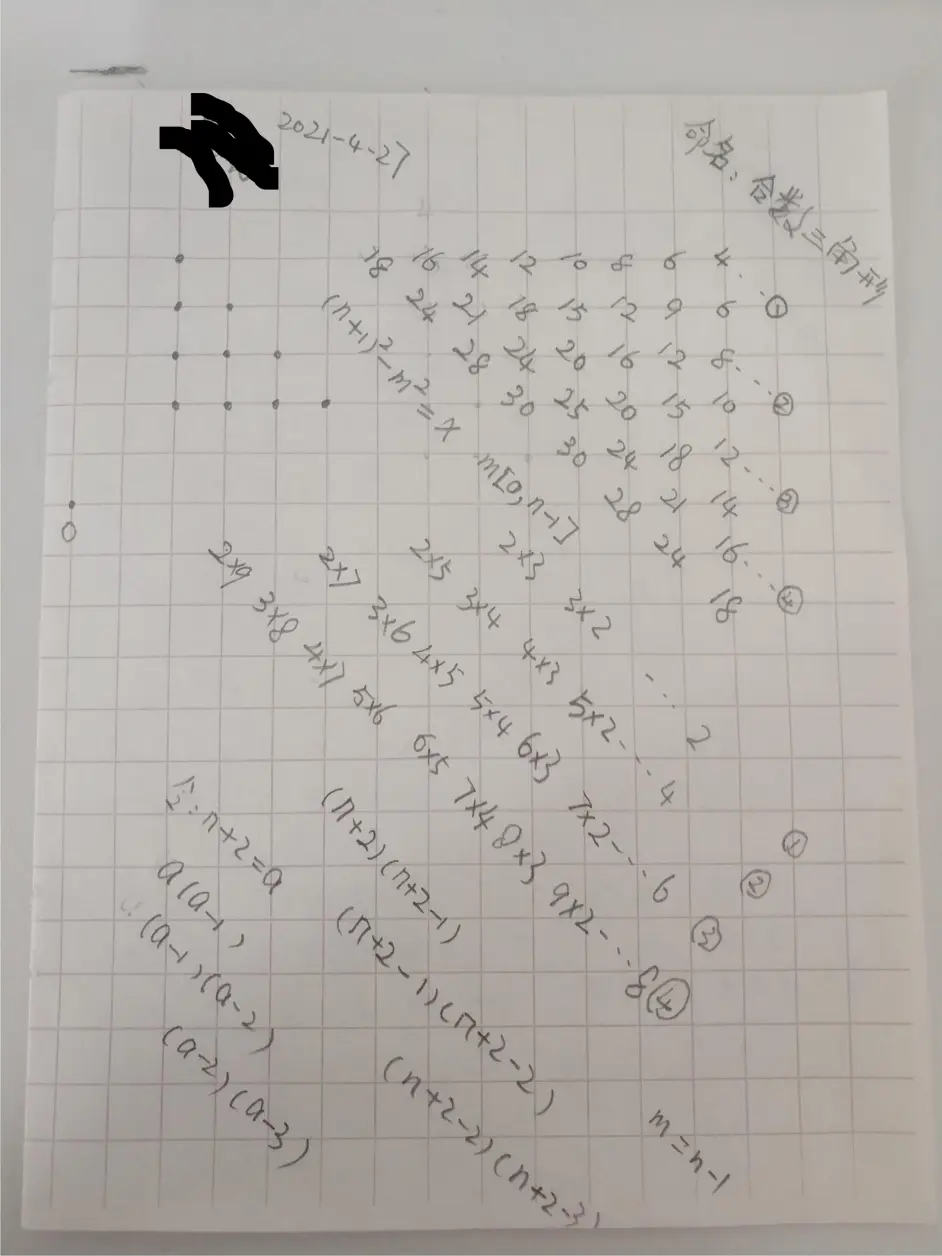
数字1 既不是质数也不是合数的几何证明 合数三角形 N Pq的分解公式 哔哩哔哩

算法讲解 质数判断及质因数分解 阿维斯托 博客园

Incoming Term: 数1 因数分解, 数1 因数分解 問題, 数1 因数分解 三次式, 数1 因数分解 交代式, 数1 因数分解 難問, 数1 因数分解 応用, 数1 因数分解 たすき掛け, 数1 因数分解 応用 コツ, 数1 因数分解 難しい, 数1 因数分解公式,